単結晶金属配線で発現する細線効果の異方性予測技術

2024年12月24日

回路の集積度向上に向け、多結晶で構成される金属配線の寸法を縮小すると、配線の電気抵抗が断面積の縮小以上に上昇します^[1]。これを細線効果と呼び、その主な原因は電流を運ぶ電子が金属／絶縁膜界面で散乱される回数が増えるためと考えられています。

次世代製品開発において、プロセス開発としては抵抗上昇を抑制すること、回路設計においては細線効果を予測することが課題となります。微細化が進む金属配線における抵抗上昇の抑制には、配線を構成する金属の粒界を減らすことが有効です。しかし、結晶粒界を減らして配線を単結晶化すると、細線効果が結晶方位によって大きく変化するようになります^[2]。本稿ではこれを、細線効果の異方性と呼びます。欠陥低減技術が進み、将来単結晶化された配線を使う場合、この方位依存性を事前に把握して回路設計をする必要が生じます。そこで私たちは、単結晶化によって生じる細線効果の結晶方位依存性を予測するための計算技術を新たに開発しました^[3]。

図1に計算技術の模式図を示します。細線効果の原因は、電流を運ぶ自由電子の運動を特徴づける“フェルミ速度”に方向的な分布があることです。電流を運ぶ電子はフェルミ速度で走行しており、このフェルミ速度に異方性があると、細線効果の主要因である電子の界面散乱に異方性が生じ、その結果、細線効果にも異方性が生じることになります。

私たちは結晶構造・材料に依存したフェルミ速度の異方性を第一原理計算手法で正確に計算して、そのフェルミ速度分布に従って配線中の電子運動を模擬する粒子シミュレーション手法を新たに開発しました。この手法では、実空間中と波数空間中における電子の運動を、物理法則に基づいてシミュレーションします。その結果、細線効果の異方性の原因である、配線の結晶方位によって界面散乱の回数が異なるという現象を自然な形で取り込むことができます。

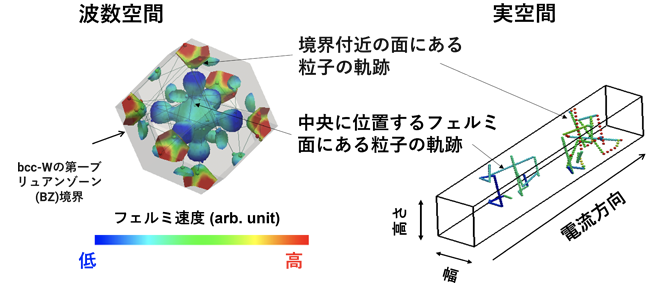
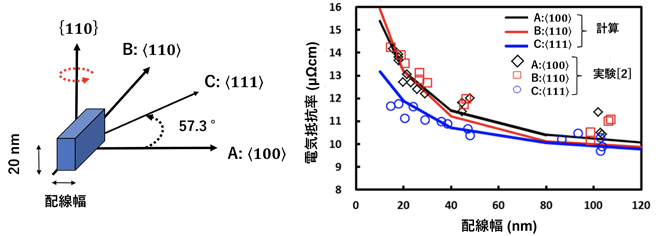
図2に、単結晶タングステン配線における細線効果の異方性の計算結果と、実験結果[2]の比較を示します。本計算技術では、単結晶タングステン配線で観察された抵抗率の配線幅・結晶方位依存性をよく再現できていることがわかります。

なお、1計算点あたりの計算時間も典型的な計算用ワークステーションで10分程度と高速です。また、この手法はタングステン以外の材料にも容易に応用できる実用的な方法をとっています。単結晶化された金属配線では、結晶方位が電気抵抗に影響する重要なパラメータとなってきます。この技術を活用して、単結晶配線における最適な材料・結晶方位の探索、メカニズムの解析を進めていきます。