ディープラーニングの推論処理高速化を目指した量子化アルゴリズムの開発

近年、ニューラルネットワークを使った画像認識の技術が広く普及しています。ニューラルネットワークを使い、画像データを認識する処理は推論と呼ばれます。推論では通常、数百万～数億回の積和演算を行う必要があり、処理時間の短縮と消費エネルギーの削減が課題です。推論の処理時間(以下、推論時間とします)を短縮する方法の一つに量子化*¹という手法があります。弊社はこれまでにニューラルネットワークの各層に数十～数千あるフィルタと呼ばれるブロックごとに、別々の重みビット数を割り当てる量子化アルゴリズムおよびその専用のハードウェア構成を開発してきました^[1][2]。これらの技術を活用することで、認識精度を維持したまま推論時間を短縮することが可能になります。このとき層やフィルタごとに独立して存在するそれぞれの重みにいかに最適なビット数を割り当てられるかが鍵となります(図1上段)。

従来手法^[3]では、学習を通して最適なビット数の割り当てを見つけ出します。通常、ニューラルネットワークは、入力された画像データを正しく認識できるように、すなわち認識の誤りがなくなるように、重みの値を繰り返し調整し、最適な重みの値を見つけ出します。この重みの値の調整に加えて、従来手法^[3]では、認識の誤りをなくすという条件と重みのデータ量*²を小さくするという条件の下、ビット数の割り当てを繰り返し調整し、最適なビット数の割り当てを見つけ出します(図1左下)。

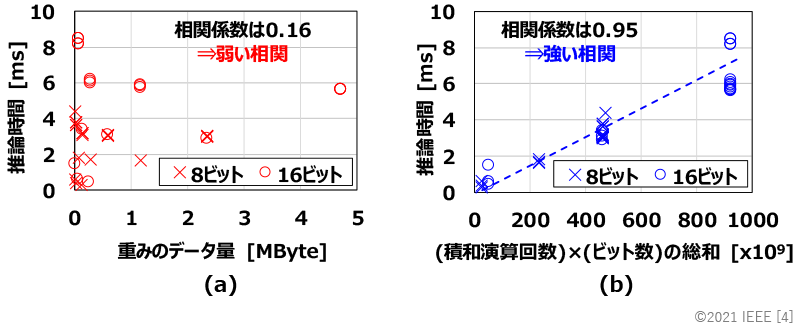
この手法は、例えば重みのデータ量をなるべく少なく抑えつつ、高い認識精度を実現する重みの値とビット数の割り当てを見つけたい場合に有効です。しかしながら、図2(a)に示すように、重みのデータ量と推論時間の相関は弱く、仮に重みのデータ量を小さくできたとしても、推論時間が短くなるとは限りません。そのため、従来手法^[3]は、推論時間を短縮するという観点では最適ではありませんでした。

そこで、今回提案する技術では、重みのデータ量(ビット数)だけでなく、積和演算の回数も考慮した、積和演算の回数とビット数の積の総和に着目します。図2(b)に示すように、積和演算の回数と重みのビット数で積を取り、全重み分、足し合わせた値は推論時間と強い相関があり、この総和の値を小さくすることで推論時間を短縮することができます。この事実に基づき、学習時に認識の誤りをなくすという条件と積和演算の回数とビット数の積の総和を小さくするという条件の下、重みの値とビット数の割り当てを繰り返し調整します(図1右下)。その結果、短い推論時間で高い認識精度を実現するための最適な設定を見つけることができます。

提案手法をResNet-18*³というニューラルネットワークの重みの値とビット数の割り当ての調整に適用し評価した結果を表1に示します。今回、認識精度の評価にはImageNet*⁴という画像データセットを使用し、推論時間の評価には弊社で開発したハードウェア構成^[1]を使用しました。表1に示すように、従来手法^[3]で調整を行った場合と同等となる70.0%の認識精度を維持しつつ、平均ビット数を1.4ビット低減し、推論時間を約21%短縮することに成功しました。