Effective Implementation of Flash Memory and New Algorithm to Speed Up Approximate Nearest Neighbor Search Method (Locality Sensitive Hashing)

June 14, 2023

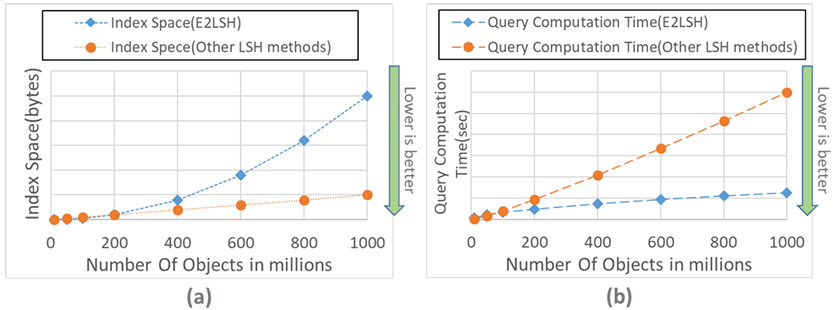
Nearest neighbor search is one of the most important data processing operations and used in various applications such as database processing, text search, and pattern recognition. This performance strongly effects the overall performance of the application.　Since exact nearest neighbor search is computationally expensive, approximate methods are generally used. One of these approximate methods is Locality Sensitive Hashing (LSH). It is widely used because of its theoretically guaranteed success probability, a feature not found in other approximate methods, and its ability to achieve practical query speed. The early work on LSH in the Euclidean space, E2LSH^[1], has the advantage that the computational cost of a query (the process of finding objects in the database that are close to the query target) is sub-linear, i.e., the more data there are, the slower the growth of the computational cost. On the other hand, it has the disadvantage that the index space is super-linear, which means that the data index size increases geometrically. Since the data index was too large to be stored in DRAM, it had to be placed on external storage such as SSD or HDD, and access to the index caused significant performance degradation. Subsequent LSH research (e.g., SRS^[2]) has moved in the direction of keeping the data index size small enough to be stored in DRAM　and achieved solid execution performance while maintaining theoretical guarantees.　However, they had to lose the advantage that the query computation volume (Figure 1 (b)) is sublinear although the index size is small (Figure 1 (a)).

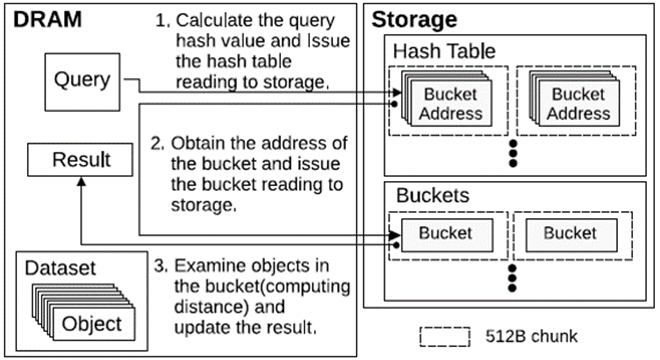
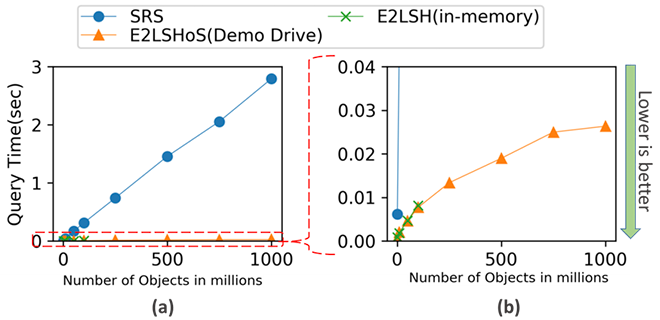
In this time, we developed E2LSH on Storage (E2LSHoS), a newly developed algorithm for utilizing E2LSH on flash memory, and evaluated it on a large data set of up to 1 billion data items (maximum data index size of approximately 7 TB). To take advantage of the parallel reads of SSDs, E2LSHoS is designed for asynchronous access and parallel execution of multiple queries by allocating the large data indexes to external storage and the other data to main memory (Figure 2). This allows the algorithm to achieve higher performance than the state-of-arts LSH method, SRS as the data set size increases thanks to the advantage of sublinear query speed. To demonstrate the performance of this algorithm, we used a demo drive^[3] using low-latency flash XL-FLASH™, which can issue over 1 million storage access requests per second from a single CPU core, as external storage and we showed that E2LSHoS keeps sub-linear query speeds and achieved the performance equivalent to E2LSH where whole data stored entirely in DRAM. (Figure 3).
This result is an example of our low-latency flash supporting a small computation algorithm. We believe that E2LSHoS is becoming more and more valuable in recent years as the amount of data is increasing day by day. We also believe that it is applicable to other algorithms with similar characteristics.