Development of quantization algorithm for accelerating deep learning inference

Deep neural networks are widely used for image recognition tasks in recent years. The process to recognize input images with deep neural networks is called inference. An inference requires millions to billions of multiply-accumulate (MAC) operations, therefore the reduction of the processing time and energy consumption is a challenge. Quantization*¹ is one of the methods to reduce the processing time for inference (hereinafter referred to as inference time). We have developed not only a filter-wise quantization algorithm which optimizes the number of weight bits for each one of tens or thousands of filters on every layer but also the dedicated accelerator^[1][2]. With these  algorithm and hardware architecture, the inference time can be reduced while maintaining recognition accuracy. It is important to allocate the optimal number of bits to weights depending on each layer or filter (upper part of Fig. 1).

A conventional method^[3] finds out the optimal bit allocations through training. Generally, weight values are tuned iteratively to recognize input image data correctly, in other words to minimize recognition error. After training, we can obtain optimized weight values. In addition to this weight optimization, the conventional method^[3] optimizes bit allocation by tuning the bit allocation iteratively under the condition of minimizing the recognition error and data size of weights*² (lower left of Fig. 1).

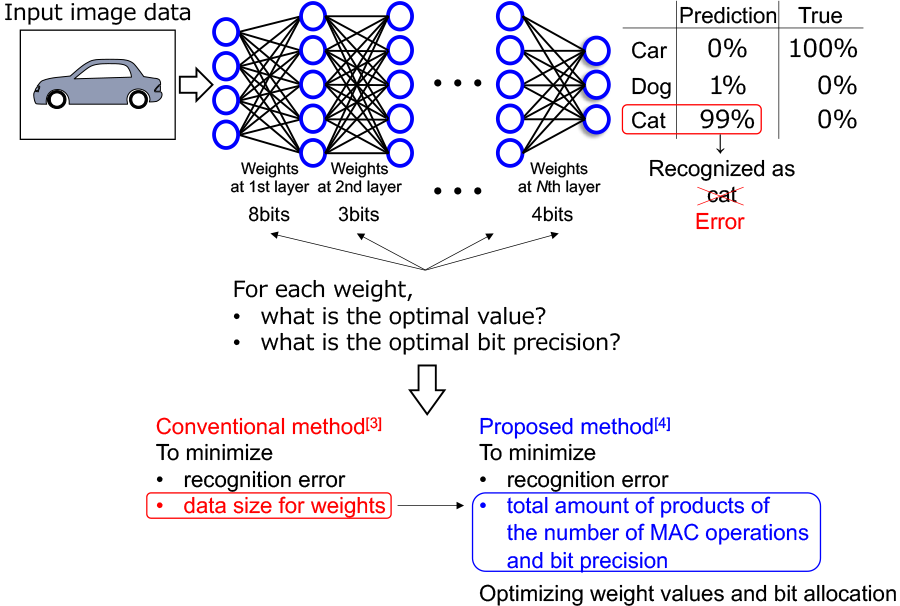
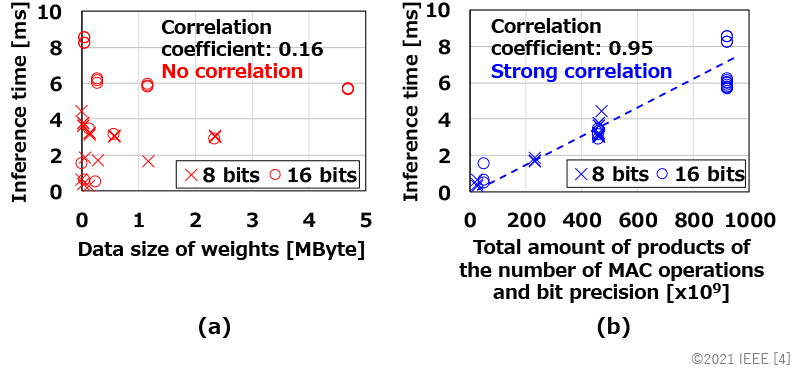
After the optimization, we can obtain the optimized bit allocation. This method is effective to find weight values and bit allocation which achieve better recognition accuracy with less total data size of weights. As shown in Fig. 2(a), however, there is no strong correlation between the data size of weights and inference time, and the inference time is not always reduced even if the data size of weights becomes smaller. Therefore, the conventional method^[3] is not optimal for reducing inference time.

Here, we focus on a metric which accumulates products of the number of MAC operations and bit precision. This metric includes the number of MAC operations as well as the number of bit precision, considering the impact of MAC operations to inference time. As shown in Fig. 2(b), this metric strongly correlates with inference time, and the inference time can be reduced if the metric value becomes smaller. Based on this result, we optimize weight values and bit allocation under the condition of minimizing the recognition error and the metric value (lower right of Fig. 1). Consequently, we can obtain optimized weight values and bit allocation for achieving better recognition accuracy with less inference time.

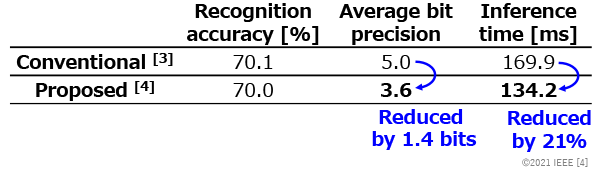
We applied the proposed method to the optimization for weight values and bit allocation of the ResNet-18*³ model. We evaluated the recognition accuracy with the ImageNet*⁴ dataset and the inference time with our dedicated accelerator^[1]. As shown in Table 1, the optimized model by our proposed method achieves 70.0% recognition accuracy, which is almost the same as the optimized one by the conventional method, while reducing the average bit precision by 1.4 bits and the inference time by 21%.